Lets formalize the technique that can be used when solving overlapping puzzles, which I have been referring to as “the new solving technique” and that I now call Twin Nonets.
Basically, this technique is a sub-technique (or if you like – a consequence) of the naked/hidden triplets technique that you are all probably aware of. But, naked/hidden triplets are sometimes difficult to spot and this is very obvious once you realize what it’s all about.
The technique only applies to overlapping puzzles where two sub-puzzles overlap on at least two nonets. So it doesn’t apply to puzzles like Samurai. It applies to Flower Sudoku, Butterfly Sudoku, Double Sudoku, Triple Sudoku and other puzzles that I have posted before.
So after all this talk lets get to the point. Here is the first Double Trouble X that I posted a while ago:
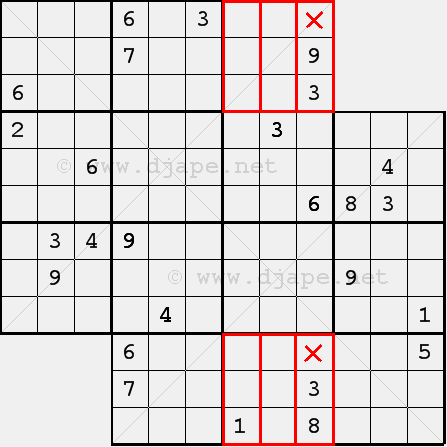
The nonets highlighted in red are twin nonets. This means that 3 triplets that constitute each nonet must contain the same numbers as in the matching triplet in the twin nonet (not always in the same order). So, the cells that are marked with a red “x” must be 8 and 9 respectively. Why? Because in the matching triplets we have those numbers so they must be there and there is only one spot where they can fall into.
What’s also important to know is that you can use this rule to eliminate candidates from a cell. I’m using the same example. Look at the left triplets of the highlighted nonets. In the bottom red nonet, there is number 1 in the left triplet. Therefore, this number must be somewhere in the left triplet of the top red nonet, which means that it can be eliminated as a candidate from the middle triplet of the top red nonet! I know this now looks obvious, but sometimes it’s easy to miss. For example, in the Triple X puzzle that I posted before, it’s difficult to see this (see the comments bellow Triple X post).
In double trouble X puzzles there are 4 pairs of twin nonets. I showed you one and I’m sure that you can see what other three are. However, because this is an “X” puzzle, there is another Twin Triplets pair and it’s on the long diagonal (12 cells). The three cells from nonet 1 and the three cells from the bottom-right nonet must contain the same numbers (again – not necessarily in the same order).

















0 Comments